Loads of websites, articles and research papers are written about PHI and the golden ratio, and as many photo’s showing it being expressed in flowers, pine cones, shells, galaxies and even the human body, its relation to the Fibonacci Series Algorithm and it being part of ancient knowledge. But no-where do you find anything on HOW it comes about, we are given the impression that science knows because it can calculate its value, but far from it, they have no clue as to how it comes about in nature.
So let’s look at what they do know first.
Phi is the basis for the Golden Ratio, Section or Mean. The ratio, or proportion, determined by Phi (1.618 …) was known to the Greeks as the “dividing a line in the extreme and mean ratio” and to Renaissance artists as the “Divine Proportion”. It is also called the Golden Section, Golden Ratio and the Golden Mean.
Here a piece from Wikipedia:
Some historians consider that the history of the golden ratio begins when this value was the subject of a specific study. For others, the determination of a geometric figure containing at least a proportion calculated using the golden ratio is sufficient. The Pyramid of Cheops (around 2600 BC.) Becomes, in the latter agreement, a good candidate for the origin
Historians all agree on the existence of an ancient origin , but the absence of a document from the final period prohibits an indisputable knowledge of the origin 8 . In this context, the assumption is sometimes made that the golden ratio has its origin in the Pythagoreans : they would have known and built the regular dodecahedron.
The Pythagoreans already knew of a construction of the pentagon using isosceles triangles . At that time, the study of the golden section is essentially geometric, Hypsicles , a Greek mathematician ii century BC. AD , in fact used for the measurement of regular polyhedra . It returns each time a pentagon is present.
The arithmetic approach is initially blocked by the Pythagorean prejudice which would like any number to be rational (remember that the golden ratio is not). Plato evokes this difficulty . The first evidence of the irrationality of some diagonals of regular polygons back probably to v th century BC. AD . Plato cites the works of his tutor, Theodore of Cyrene , which shows the irrationality of √ 5 and, consequently, that of the golden ratio .From this time, Greek mathematicians discovered algorithms for approximating diagonal and lateral numbers . Much later, Hero of Alexandria , a mathematician Some historians consider that the history of the golden ratio begins when this value was the subject of a specific study. For others, the determination of a geometric figure containing at least a proportion calculated using the golden ratio is sufficient. The Pyramid of Cheops (around 2600 BC.) .
Historians all agree on the existence of an ancient origin , but the absence of a document from the final period prohibits an indisputable knowledge of the origin . In this context, the assumption is sometimes made that the golden ratio has its origin in the Pythagoreans : they would have known and built the regular dodecahedron.
The Pythagoreans already knew of a construction of the pentagon using isosceles triangles . At that time, the study of the golden section is essentially geometric, Hypsicles , a Greek mathematician ii century BC. AD , in fact used for the measurement of regular polyhedra 7 . It returns each time a pentagon is present.
The arithmetic approach is initially blocked by the Pythagorean prejudice which would like any number to be rational (remember that the golden ratio is not). Plato evokes this difficulty . The first evidence of the irrationality of some diagonals of regular polygons back probably to v th century BC. AD . Plato cites the works of his tutor, Theodore of Cyrene , which shows the irrationality of √ 5 and, consequently, that of the golden ratio .From this time, Greek mathematicians discovered algorithms for approximating diagonal and lateral numbers . Much later, Hero of Alexandria , a mathematician i st century furthers this approach by using tables trigonometric of Ptolemy
The first indisputable mathematical text is that of the Elements of Euclid (circa 300 BC). In the 3 th definition of Book vi , the golden ratio is defined as a geometrical proportion:
” A straight line is said to be cut in the extreme and middle reason when, as it is entirely relative to the largest segment, so is the largest relative to the smallest. “
Its relation with the pentagon, the icosahedron and the regular dodecahedron is highlighted. It is therefore linked to the geometric problems already solved by the Pythagoreans i , but according to the science historian Thomas Heath (based on Proclus ), it was probably Plato who then made it an object of study in itself:
The idea that Plato initiated the study (of the golden ratio ) as an intrinsic subject is not at all contradictory with the supposition that the problem of Eucl. II . It was solved by the Pythagoreans
So far Wikipedia, now there are loads of website showing it can be found in flowers, the human body, solar systems, and much much more and in 1202 AD, Leonardo Fibonacci in his book “Liber Abaci” of a simple numerical sequence that is the foundation for an mathematical relationship behind Phi. This sequence was also known as early as the 6th century AD by Indian mathematicians, but it was Fibonacci who introduced it to the west after his travels throughout the Mediterranean world and North Africa”.
Starting with 0 and 1, each new number in the sequence is simply the sum of the two before it.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 . . .
Phi ( Φ = 1.618033988749895… ), is an irrational number like pi ( p = 3.14159265358979… ), but one with many unusual mathematical properties. Unlike pi, which is a transcendental number, phi is the solution to a quadratic equation.
A circle with a diameter of 1 and circumference of pi, 3.14 Phi, like Pi, is a ratio defined by a geometric construction.
Just as pi is the ratio of the circumference of a circle to its diameter, phi is simply the ratio of the line segments that result when a line is divided in one very special and unique way. Yet they both have the same origin, the cubit.
I could fill page after page but this should be more than enough for you to see this ratio (and others mentioned in the articles). So let’s move to the cause of it, the how it comes to be! For this you need to look at the cell division again. Where the one (circle) becomes two.
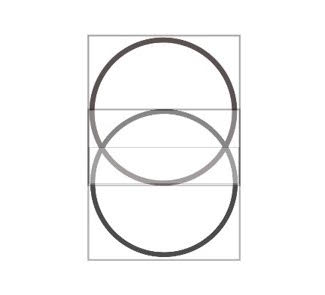
As you can see the single circle in the square is placed for half its size over the other circle so that the size if the diameter is two cubit now makes a total of 1,5 in diameter. If the radius of the circle and square is one cubit then the total height is 3 cubit. The problem here is that you cannot fit one part of the circle (say it is a solid ) in the other circle. Now imagine this space is full and I mean FULL of energy, a force, then one part must be forced out. For this reason I divided the part of the Vesica Piscis in two, or half a cubit, as you know the cubit is 5,236 therefore half a cubit is equal to 2,618, yes indeed Phi.
Now where would this energy or force escape from as there is no space for it? Right there where the circles join, and at the very points where the hexagram and pentagram join with its 60 and 36 degrees making 96.
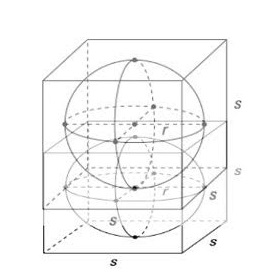
The first drawing was a 2D presentation, above you have the 3D version of it.
But let’s remember that the eight rotates within the bigger circle and now look at how this force would look like, taking that in consideration.
Although this drawing isn’t correct you will get the idea and see it reflected in the galaxies and how the Yin-Yang sign represents these two opposing forces and originates from the same knowledge.
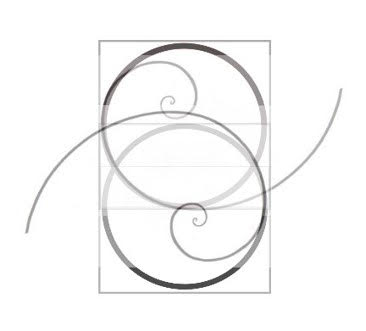
While the math is a bit more complicated than is presented here, it is sufficient for the purpose of this article.
Over the years more and more researchers have come to see that this structure plays a vital role in the creation of matter and the universe. While they all like to give it their own twist and name, very few are willing to look at a way to join forces, as each branch of science would find their questions answered in it. Which brings us to the real important issue here, and that is that we are made in his image therefore looking within makes us see what is out there. And I would like to say, I think therefore I am NOT(hing) but a passing of a shadow on the wall of Plato’s cave.
If we really want to make this big evolutionary jump we will need to embrace this inner science with all our might.
31-03-2018
Moshiya van den Broek
