“Behind it all is surely an idea so simple, so beautiful, so compelling that when in a decade, a century or a millennium we grasp it, we will all say to each other, how could it be otherwise? How could we have been so stupid for so long?” Professor John Archibald Wheeler.

The fundamental questions of cosmology and particle physics are of a very special type. Any explanation for the origin and structure of the universe is likely to be of a very unusual sort, we would be foolish to discard certain approaches to these problems simply because they do not have an analogues in more mundane scientific investigation. Professor John D. Barrow.

Man cannot look at reality with just one brain half, which is what takes place in the mathematical analyses in quantum mechanics.

Before explaining the nature of black holes and the illusion of matter please read the article on Wikipedia.
While some of it will be difficult to grasp without the scientific background, it is not needed other than the basic principles, as I will explain it in simple terms after this article.

Looking for the theory of everything, scientists forget that the answer should be simple and logical, but their theories become more and more complex and each time they have to create new theories to try and solve the black holes in their theories.

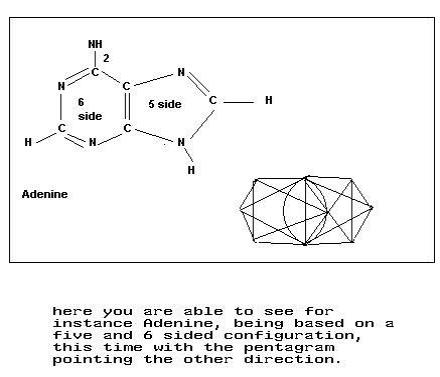
A theory of everything (TOE) is a putative theory of theoretical physics that would fully explain and link together all known physical phenomena. One thing before you start reading the article below which as you will see turns out to lead to the “theory” of everything is something that nature shows “SYMMETRY”. Symmetry is mathematically so important in the solution because nature into its smallest has the tendency to be symmetrically shaped, just cut an apple in two and see the configuration of its seeds in the shape of a pentagram, the golden ratio in branches, flowers, or what seems to be more basic shapes like spheres, the platonic solids etc.

Next to this of course, the strong and weak nuclear forces, Gravity and electromagnetic forces.

Science idea of black hole.

Please do not skip this part and hold this picture in mind.

A Black hole is a theoretical region of space in which the gravitational field is so powerful that nothing, not even electromagnetic radiation (e.g. visible light), can escape its pull after having fallen past its event horizon. The term derives from the fact that the absorption of visible light renders the hole’s interior invisible, and indistinguishable from the black space around it. Despite its interior being invisible, a black hole may reveal its presence through an interaction with matter that lies in orbit outside its event horizon. For example, a black hole may be perceived by tracking the movement of a group of stars that orbit its centre. Alternatively, one may observe gas (from a nearby star, for instance) that has been drawn into the black hole. The gas spirals inward, heating up to very high temperatures and emitting large amounts of radiation that can be detected from earthbound and earth-orbiting telescopes. [2] [3] Such observations have resulted in the general scientific consensus that—barring a breakdown in our understanding of nature—black holes do exist in our universe.[4]

The idea of an object with gravity strong enough to prevent light from escaping was proposed in 1783 by John Michell, an amateur British astronomer. In 1795, Pierre-Simon Laplace, a French physicist independently came to the same conclusion.

Black holes, as currently understood, are described by the general theory of relativity. This theory predicts that when a large enough amount of mass is present in a sufficiently small region of space (Hoop conjecture), all paths through space (world line) are warped inwards towards the centre of the volume, preventing all matter and radiation within it from escaping.

While general relativity describes a black hole as a region of empty space with a point-like singularity at the centre and an event horizon at the outer edge, the description changes when the effects of quantum mechanics are taken into account.

Research on this subject indicates that, rather than holding captured matter forever, black holes may slowly leak a form of thermal energy called Hawking radiation and may well have a finite life.  However, the final, correct description of black holes, requiring a theory of quantum gravity, is unknown.

Popular accounts commonly try to explain the black hole phenomenon by using the concept of escape velocity, the speed needed for a vessel starting at the surface of a massive object to completely clear the object’s gravitational field. It follows from Newton’s law of gravity that a sufficiently dense object’s escape velocity will equal or even exceed the speed of light. Citing that nothing can exceed the speed of light they then infer that nothing would be able to escape such a dense object. However, the argument has a flaw in that it does not explain why light would be affected by a gravitating body or why it would not be able to escape. Nor does it give a satisfactory explanation for why a powered spaceship would not be able to break free.

Two concepts introduced by Albert Einstein are needed to explain the phenomenon.

The first is that time and space are not two independent concepts, but are interrelated forming a single continuum, spacetime. This continuum has some special properties. An object is not free to move around spacetime at will; it must always move forward in time and cannot change its position in space faster than the speed of light. This is the main result of the theory of special relativity.

The second concept is the base of general relativity; mass deforms the structure of this spacetime. The effect of a mass on spacetime can informally be described as tilting the direction of time towards the mass. As a result, objects tend to move towards masses. This is experienced as gravity. This tilting effect becomes more pronounced as the distance to the mass becomes smaller. At some point close to the mass, the tilting becomes so strong that all the possible paths an object can take lead towards the mass. This implies that any object that crosses this point can no longer get further away from the mass, not even using powered flight. This point is called the event horizon.

Properties: mass, charge and angular momentum

According to the “No Hair” theorem a black hole has only three independent physical properties: mass, charge and angular momentum. Any two black holes that share the same values for these properties are indistinguishable. This contrasts with other astrophysical objects such as stars, which have very many—possibly infinitely many—parameters. Consequently, a great deal of information is lost when a star collapses to form a black hole. Since in most physical theories information is preserved (in some sense), this loss of information in black holes is puzzling. Physicists refer to this as the black hole information paradox.

The “No Hair” theorem does make some assumptions about the nature of our universe and the matter it contains. Other assumptions would lead to different conclusions. For example, if nature allows magnetic monopoles to exist—which appears to be theoretically possible, but has never been observed—then it should also be possible for a black hole to have a magnetic charge. If the universe has more than four dimensions (as string theories, a controversial but apparently possible class of theories, would require), or has a global anti-de Sitter structure, the theorem could fail completely, allowing many sorts of “hair”. However, in our apparently four-dimensional, very nearly flat universe, the theorem should hold.

Black hole types

The simplest possible black hole is one that has mass but neither charge nor angular momentum. These black holes are often referred to as Schwarzschild black holes after the physicist Karl Schwarzschild who discovered this solution in 1915. It was the first (non-trivial) exact solution to the Einstein equations to be discovered, and according to Birkhoff’s theorem, the only vacuum solution that is spherically symmetric. For real world physics this means that there is no observable difference between the gravitational field of such a black hole and that of any other spherical object of the same mass—for example a spherical star or planet—once one is in the empty space outside the object. The popular notion of a black hole “sucking in everything” in its surroundings is therefore incorrect; the external gravitational field, far from the event horizon, is essentially like that of ordinary massive bodies.

More general black hole solutions were discovered later in the 20th century. The Reissner-Nordström solution describes a black hole with electric charge, while the Kerr solution yields a rotating black hole. The most general known stationary black hole solution is the Kerr-Newman metric, having both charge and angular momentum. All these general solutions share the property that they converge to the Schwarzschild solution at distances that are large compared to the ratio of charge and angular momentum to mass (in natural units).

While the mass of a black hole can take any (positive) value, the other two properties, charge and angular momentum, are constrained by the mass. In natural units , the total charge Q and the total angular momentum J are expected to satisfy Q2+(J/M)2 ? M2 for a black hole of mass M. Black holes saturating this inequality are called extremal.

Solutions of Einstein’s equation violating the inequality do exist, but do not have a horizon. These solutions have naked singularities and are thus deemed unphysical.

The cosmic censorship hypothesis states that it is impossible for such singularities to form in due to gravitational collapse of generic realistic matter. This is supported by numerical simulations.

Black holes forming from the collapse of stars are expected—due to the relatively large strength of electromagnetic force—to retain the nearly neutral charge of the star. Rotation, however, is expected to be a common feature of compact objects, and the black-hole candidate binary X-ray source GRS 1915+105  appears to have an angular momentum near the maximum allowed value.

Sizes

Black holes occurring in nature are commonly classified according to their mass, independent of angular momentum J. The size of a black hole, as determined by the radius of the event horizon, or Schwarzschild radius, is proportional to the mass M through

where Rsh is the Schwarzschild radius and Mo is the mass of the Sun.

Thus, size and mass have a simple relationship, which is independent of rotation. According to this mass/size criterion then, black holes are commonly classified as:

• Supermassive black holes that contain hundreds of thousands to billions of solar masses are believed to exist in the centre of most galaxies, including our own Milky Way. They are thought to be responsible for active galactic nuclei, and presumably form either from the coalescence of smaller black holes, or by the accretion of stars and gas onto them. The largest known supermassive black hole is located in OJ 287 weighing in at 18 billion solar masses.

• Intermediate-mass black holes, whose sizes are measured in thousands of solar masses, probably exist. They have been proposed as a possible power source for the ultra-luminous X ray sources. There is no known mechanism for them to form directly, so they most probably form via collisions of lower mass black holes, either in the dense stellar cores of globular clusters or galaxies. Such creation events should produce intense bursts of gravitational waves, which may be observed in the near- to mid-term. The boundary limit between super and intermediate-mass black holes is a matter of convention. Their lower mass limit, the maximum mass for direct formation of a single black hole from collapse of a massive star, is poorly known at present.

• Stellar-mass black holes have masses ranging from a lower limit of about 1.5– 3.0 solar masses (the Tolman-Oppenheimer-Volkoff limit for the maximum mass of neutron stars) up to perhaps 15–20 solar masses, and are created by the collapse of individual stars, or by the coalescence (inevitable, due to gravitational radiation) of binary neutron stars. Stars may form with initial masses up to ? 100 solar masses, or possibly even higher, but these shed most of their outer massive layers during earlier phases of their evolution, either blown away in stellar winds during the red giant, AGB, and Wolf-Rayet stages, or expelled in supernova explosions for stars that turn into neutron stars or black holes. Being known mostly by theoretical models for late-stage stellar evolution, the upper limit for the mass of stellar-mass black holes is somewhat uncertain at present. The cores of still lighter stars form white dwarfs.

• Micro black holes (also mini black holes) have masses much less than that of a star. At these sizes, the effects of quantum mechanics are expected to come into play. There is no known mechanism for them to form via normal processes of stellar evolution, but certain inflationary scenarios predicted their production during the early stages of the evolution of the universe. According to some theories of quantum gravity they may also be produced in the highly energetic reaction produced by cosmic rays hitting the atmosphere or even in particle accelerators such as the Large Hadron Collider. The theory of Hawking radiation predicts that such black holes will evaporate in bright flashes of gamma radiation. NASA’s Fermi Gamma-ray Space Telescope satellite (formerly GLAST), launched in 2008, will search for such flashes as one of its scientific objectives.

Features

Event horizon

The defining feature of a black hole, the event horizon, is a surface in spacetime that marks a point of no return. Once an object has crossed this surface there is no way that it can return to the other side. Consequently, anything inside this surface is completely hidden from observers outside. Other than this the event horizon is a completely normal part of space, with no special features that would allow someone falling into the a black hole to know when he would cross the horizon. The event horizon is not a solid surface, and does not obstruct or slow down matter or radiation that is traveling towards the region within the event horizon.

Outside of the event horizon, the gravitational field is identical to the field produced by any other spherically symmetric object of the same mass. The popular conception of black holes as “sucking” things in is false: objects can maintain an orbit around black holes indefinitely, provided they stay outside the photon sphere (described below), and also ignoring the effects of gravitational radiation, which causes orbiting objects to lose energy, similar to the effect of electromagnetic radiation.

Singularity

According to general relativity, there is a space-time singularity at a centre of a spherical black hole, which means an infinite space-time curvature. It means that from a point of view of an observer which falls into a black hole, in a finite time (at the end of his fall) a black hole’s mass becomes entirely compressed into a region with zero volume, so its density becomes infinite. This zero-volume, infinitely dense region at the centre of a black hole is called a gravitational singularity.

The singularity in a non-rotating black hole is a point, in other words it has zero length, width, and height. The singularity of a rotating black hole is smeared out to form a ring shape lying in the plane of rotation. The ring still has no thickness and hence no volume.

The appearance of singularities in general relativity is commonly perceived as signalling the breakdown of the theory. This breakdown is not unexpected, as it occurs in a situation where quantum mechanical effects should become important, since densities are high and particle interactions should thus play a role.

Unfortunately, to date it has not been possible to combine quantum and gravitation effects in a single theory. It is however quite generally expected that a theory of quantum gravity will feature black holes without singularities.

Note, however, that formation of the singularity takes finite (and very short) time only from the point of view of an observer which resides in collapsing object. From the point of view of distant observer, it takes infinite time to do so due to gravitational time dilation.

Photon sphere

The photon sphere is a spherical boundary of zero thickness such that photons moving along tangents to the sphere will be trapped in a circular orbit. For nonrotating black holes, the photon sphere has a radius 1.5 times the Schwarzschild radius. The orbits are dynamically unstable, hence any small perturbation (maybe caused by some infalling matter) will grow over time, either setting it on an outward trajectory escaping the black hole or on an inward spiral eventually crossing the event horizon.

While light can still escape from inside the photon sphere, any light that crosses the photon sphere on an inbound trajectory will be captured by the black hole. Hence any light reaching an outside observer from inside the photon sphere must have been emitted by objects inside the photon sphere but still outside of the event horizon.

Other compact objects, such as neutron stars, can also have photon spheres. This follows from the fact that the gravitation field of an object does not depend on its actual size, hence any object that is smaller than 1.5 times the Schwarzschild radius corresponding to its mass will in fact have a photon sphere.

Ergosphere

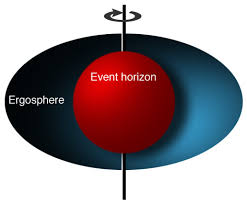
The ergosphere is an oblate spheroid region outside of the event horizon, where objects cannot remain stationary.

Rotating black holes are surrounded by a region of spacetime in which it is impossible to stand still, called the ergosphere. This is the result of a process known as frame-dragging; general relativity predicts that any rotating mass will tend to slightly “drag” along the spacetime immediately surrounding it. Any object near the rotating mass will tend to start moving in the direction of rotation. For a rotating black hole this effect becomes so strong near the event horizon that an object would have to move faster than the speed of light in the opposite direction to just stand still.

The ergosphere of black hole is bounded by
• on the outside, an oblate spheroid, which coincides with the event horizon at the poles and is noticeably wider around the “equator”. This boundary is sometimes called the “ergosurface”, but it is just a boundary and has no more solidity than the event horizon. At points exactly on the ergosurface, spacetime is “dragged around at the speed of light.”
• on the inside, the (outer) event horizon.

Within the ergosphere, space-time is dragged around faster than light—general relativity forbids material objects to travel faster than light (so does special relativity), but allows regions of space-time to move faster than light relative to other regions of space-time.

Objects and radiation (including light) can stay in orbit within the ergosphere without falling to the centre. But they cannot hover (remain stationary, as seen by an external observer), because that would require them to move backwards faster than light relative to their own regions of space-time, which are moving faster than light relative to an external observer.

Objects and radiation can also escape from the ergosphere. In fact the Penrose process predicts that objects will sometimes fly out of the ergosphere, obtaining the energy for this by “stealing” some of the black hole’s rotational energy. If a large total mass of objects escapes in this way, the black hole will spin more slowly and may even stop spinning eventually.

Hawking radiation

In 1974, Stephen Hawking showed that black holes are not entirely black but emit small amounts of thermal radiation. He got this result by applying quantum field theory in a static black hole background. The result of his calculations is that a black hole should emit particles in a perfect black body spectrum. This effect has become known as Hawking radiation. Since Hawking’s result many others have verified the effect through various methods.

The temperature of the emitted black body spectrum is proportional to the surface gravity of the black hole. For a Schwarzschild black hole this is inversely proportional to the mass. Consequently, large black holes are very cold and emit very little radiation. A stellar black hole of 10 solar masses, for example, would have a Hawking temperature of several nanokelvin, much less than the 2.7K produced by the Cosmic Microwave Background. Micro black holes on the other hand could be quite bright producing high energy gamma rays.

Due to low Hawking temperature of stellar black holes, Hawking radiation has never been observed at any of the black hole candidates.

Effects of falling into a black hole

Spaghettification

An object in any very strong gravitational field feels a tidal force stretching it in the direction of the object generating the gravitational field. This is because the inverse square law causes nearer parts of the stretched object to feel a stronger attraction than farther parts. Near black holes, the tidal force is expected to be strong enough to deform any object falling into it, even atoms or composite nucleons; this is called spaghettification. The process of spaghettification is as follows. First, the object that is falling into the black hole splits in two. Then the two pieces each split themselves, rendering a total of four pieces. Then the four pieces split to form eight. This process of bifurcation continues up to and past the point in which the split-up pieces of the original object are at the order of magnitude of the constituents of atoms. At the end of the spaghettification process, the object is a string of elementary particles.

The strength of the tidal force of a black hole depends on how gravitational attraction changes with distance, rather than on the absolute force being felt. This means that small black holes cause spaghettification while infalling objects are still outside their event horizons, whereas objects falling into large, supermassive black holes may not be deformed or otherwise feel excessively large forces before passing the event horizon.

Before the falling object crosses the event horizon

An object in a gravitational field experiences a slowing down of time, called gravitational time dilation, relative to observers outside the field. The outside observer will see that physical processes in the object, including clocks, appear to run slowly. As a test object approaches the event horizon, its gravitational time dilation (as measured by an observer far from the hole) would approach infinity. Its time would appear to be stopped.

From the viewpoint of a distant observer, an object falling into a black hole appears to slow down, approaching but never quite reaching the event horizon: and it appears to become redder and dimmer, because of the extreme gravitational red shift caused by the gravity of the black hole. Eventually, the falling object becomes so dim that it can no longer be seen, at a point just before it reaches the event horizon. All of this is a consequence of time dilation: the object’s movement is one of the processes that appear to run slower and slower, and the time dilation effect is more significant than the acceleration due to gravity; the frequency of light from the object appears to decrease, making it look redder, because the light appears to complete fewer cycles per “tick” of the observer’s clock; lower-frequency light has less energy and therefore appears dimmer, as well as redder.

From the viewpoint of the falling object, distant objects generally appear blueshifted due to the gravitational field of the black hole. This effect may be partly (or even entirely) negated by the red shift caused by the velocity of the infalling object with respect to the object in the distance.

As the object passes through the event horizon

From the viewpoint of the falling object, nothing particularly special happens at the event horizon. In fact, there is no (local) way for him to find out whether he has passed the horizon or not. An infalling object takes a finite proper time (i.e. measured by its own clock) to fall past the event horizon. This in contrast with the infinite amount of time it takes for a distant observer to see the infalling object cross the horizon.

Inside the event horizon

The object reaches the singularity at the centre within a finite amount of proper time, as measured by the falling object. An observer on the falling object would continue to see objects outside the event horizon, blue-shifted or red-shifted depending on the falling object’s trajectory. The amount of proper time a faller experiences below the event horizon depends upon where they started from rest, with the maximum being for someone who starts from rest at the event horizon. A paper in 2007 examined the effect of firing a rocket pack within the black hole, showing that this can only reduce the proper time of a person who starts from rest at the event horizon. However, for anyone else, a judicious burst of the rocket can extend the lifetime of the faller, but overdoing it will again reduce the proper time experienced. However, this cannot prevent the inevitable collision with the central singularity.

Hitting the singularity

As an infalling object approaches the singularity, tidal forces acting on it approach infinity. All components of the object, including atoms and subatomic particles, are torn away from each other before striking the singularity. At the singularity itself, effects are unknown; it is believed that a theory of quantum gravity is needed to accurately describe events near it.

Formation and evolution

From the exotic nature of black holes, it is natural to question if such bizarre objects could actually exist in nature or that they are merely pathological solutions to Einstein’s equations. However in 1970, Hawking and Penrose proved the opposite; under generic conditions black holes are expected to form in any universe. The primary formation process for black holes is expected to be the gravitational collapse of heavy objects such as stars, but there are also more exotic processes that can lead to the production of black holes.

Gravitation collapse

Gravitational collapse occurs when an object’s internal pressure is insufficient to resist the object’s own gravity. For stars this usually occurs either because a star has too little “fuel” left to maintain its temperature, or because a star which would have been stable receives a lot of extra matter in a way which does not raise its core temperature. In either case the star’s temperature is no longer high enough to prevent it from collapsing under its own weight (the ideal gas law explains the connection between pressure, temperature, and volume).

The collapse may be stopped by the degeneracy pressure of the star’s constituents, condensing the matter in an exotic denser state. The result is one of the various types of compact star. Which type of compact star is formed depends on the mass of the remnant – the matter left over after changes triggered by the collapse (such as supernova or pulsations leading to a planetary nebula) have blown away the outer layers. Note that this can be substantially less than the original star – remnants exceeding 5 solar masses are produced by stars which were over 20 solar masses before the collapse.

If the mass of the remnant exceeds ~3-4 solar masses (the Tolman-Oppenheimer- Volkoff limit)—either because the original star was very heavy or because the remnant collected additional mass through accretion of matter)—even the degeneracy pressure of neutrons is insufficient to stop the collapse. After this no known mechanism (except maybe the quark degeneracy pressure, see quark star) is powerful enough to stop the collapse and the object will inevitably collapse to a black hole.

This gravitational collapse of heavy stars is assumed to be responsible for the formation of most (if not all) stellar mass black holes.

Creation of primordial black holes in the big bang

Gravitational collapse requires great densities. In the current epoch of the universe these high densities are only found in stars, but in the early universe shortly after the big bang densities were much greater, possibly allowing for the creation of black holes. The high density alone is not enough to allow the formation of black holes since a uniform mass distribution will not allow the mass to bunch up. In order for primordial black holes to form in such a dense medium, there must be initial density perturbations which can then grow under their own gravity. Different models for the early universe vary widely in their predictions of the size of these perturbations. Various models predict the creation of black holes, ranging from a Planck mass to hundreds of thousands of solar masses. Primordial black holes could thus account for the creation of any type of black hole.

Production in high energy collisions

Gravitational collapse is not the only process that could create black holes. In principle, black holes could also be created in high energy collisions that create sufficient density. Since classically black holes can take any mass, one would expect micro black holes to be created in any such process no matter how low the energy.

However, to date, no such events have ever been detected either directly or indirectly as a deficiency of the mass balance in particle accelerator experiments. This suggests that there must be a lower limit for the mass of black holes. Theoretically this boundary is expected to lie around the Planck mass (~1019 GeV/c2), where quantum effects are expected to make the theory of general relativity break down completely.  This would put the creation of black holes firmly out of reach of any high energy process occurring on or near the Earth. Certain developments in quantum gravity however suggest that this bound could be much lower. Some braneworld scenarios for example put the Planck mass much lower, maybe even as low as 1 TeV. This would make it possible for micro black holes to be created in the high energy collisions occurring when cosmic rays hit the earth’s atmosphere, or even maybe in the new Large Hadron Collider at CERN. These theories are however very speculative, and the creation of black holes in these processes is deemed unlikely by many specialists.

Growth

Once a black hole has formed, it can continue to grow by absorbing additional matter. Any black hole will continually absorb interstellar dust from its direct surroundings and omnipresent cosmic background radiation, but neither of these processes should significantly affect the mass of a stellar black hole. More significant contributions can occur when the black hole formed in a binary star system. After formation the black hole can then leech significant amounts of matter from its companion.

Much larger contributions can be obtained when a black hole merges with other stars or compact objects. The supermassive black holes suspected in the centre of most galaxies are expected to have formed from the coagulation of many smaller objects. The process has also been proposed as the origin of some intermediate-mass black holes.

Evaporation

If Hawking’s theory of black hole radiation is correct then black holes are expected to emit a thermal spectrum of radiation, and thereby lose mass, because according to the theory of relativity mass is just highly condensed energy (e = mc2). Black holes will thus shrink and evaporate over time. The temperature of this spectrum (Hawking temperature) is proportional to the surface gravity of the black hole, which in turn is inversely proportional to the mass. Large black holes thus emit less radiation than small black holes.

A stellar black hole of 5 solar masses has a Hawking temperature of about 12 nano Kelvin . This is far less than the 2.7 K produced by the Cosmic microwave background. Stellar mass (and larger) black holes thus receive more mass from the CMB than they emit through Hawking radiation and will thus grow instead of shrink. In order to have a Hawking temperature larger than 2.7 K (and thus be able to evaporate) a black hole needs to be lighter than the Moon (and thus have diameter of less than a tenth of a millimetre).

On the other hand if a black hole is very small the radiation effects are expected to become very strong. Even a black hole that is heavy compared to a human would evaporate in an instant. A black hole the weight of a car (~ 10-24 m) would only take a nanosecond to evaporate, during which time it would briefly have a luminosity more than 200 times that of the sun. Lighter black holes are expected to evaporate even faster, for example a black hole of mass 1 TeV/c2 would take less than 10-88 seconds to evaporate completely. Of course, for such a small black hole quantum gravitation effects are expected to play an important role and could even —although current developments in quantum gravity do not indicate so— hypothetically make such a small black hole stable.

Accretion disks and gas jets

Most accretion disks and gas jets are not clear proof that a stellar-mass black hole is present, because other massive, ultra-dense objects such as neutron stars and white dwarfs cause accretion disks and gas jets to form and to behave in the same ways as those around black holes. But they can often help by telling astronomers where it might be worth looking for a black hole. On the other hand, extremely large accretion disks and gas jets may be good evidence for the presence of supermassive black holes, because as far as we know any mass large enough to power these phenomena must be a black hole.

Strong radiation emissions

A “Quasar” Black Hole

Steady X-ray and gamma ray emissions also do not prove that a black hole is present, but can tell astronomers where it might be worth looking for one – and they have the advantage that they pass fairly easily through nebulae and gas clouds.

But strong, irregular emissions of X-rays, gamma rays and other electromagnetic radiation can help to prove that a massive, ultra-dense object is not a black hole, so that “black hole hunters” can move on to some other object. Neutron stars and other very dense stars have surfaces, and matter colliding with the surface at a high percentage of the speed of light will produce intense flares of radiation at irregular intervals. Black holes have no material surface, so the absence of irregular flares around a massive, ultra-dense object suggests that there is a good chance of finding a black hole there.

Intense but one-time gamma ray bursts (GRBs) may signal the birth of “new” black holes, because astrophysicists think that GRBs are caused either by the gravitational collapse of giant stars[31] or by collisions between neutron stars, and both types of event involve sufficient mass and pressure to produce black holes. But it appears that a collision between a neutron star and a black hole can also cause a GRB, so a GRB is not proof that a “new” black hole has been formed. All known GRBs come from outside our own galaxy, and most come from billions of light years away so the black holes associated with them are actually billions of years old.

Some astrophysicists believe that some ultraluminous X-ray sources may be the accretion disks of intermediate-mass black holes.

Quasars are thought to be the accretion disks of supermassive black holes, since no other known object is powerful enough to produce such strong emissions. Quasars produce strong emission across the electromagnetic spectrum, including UV, X-rays and gamma-rays and are visible at tremendous distances due to their high luminosity. Between 5 and 25% of quasars are “radio loud,” so called because of their powerful radio emission.

Gravitational lensing

A gravitational lens is formed when the light from a very distant, bright source (such as a quasar) is “bent” around a massive object (such as a black hole) between the source object and the observer. The process is known as gravitational lensing, and is one of the predictions of the general theory of relativity. According to this theory, mass “warps” space-time to create gravitational fields and therefore bend light as a result.

A source image behind the lens may appear as multiple images to the observer. In cases where the source, massive lensing object, and the observer lie in a straight line, the source will appear as a ring behind the massive object.

Gravitational lensing can be caused by objects other than black holes, because any very strong gravitational field will bend light rays. Some of these multiple-image effects are probably produced by distant galaxies.

Objects orbiting possible black holes

See also: Kepler problem in general relativity

A Chandra X-ray spectrum of Cygnus X-1 showing a characteristic peak near 6.4 keV due to ionized iron in the accretion disk, but the peak is gravitationally red-shifted, broadened by the Doppler effect, and skewed toward lower energies.

Objects orbiting black holes probe the gravitational field around the central object. An early example, discovered in the 1970s, is the accretion disk orbiting the putative black hole responsible for Cygnus X-1, a famous X-ray source. While the material itself cannot be seen directly, the X rays flicker on a millisecond time scale, as expected for hot clumpy material orbiting a ~10 solar-mass black hole just prior to accretion. The X-ray spectrum exhibits the characteristic shape expected for a disk of orbiting relativistic material, with an iron line, emitted at ~6.4 keV, broadened to the red (on the receding side of the disk) and to the blue (on the approaching side).

Another example is the star S2, seen orbiting the Galactic centre. Here the star is several light hours from the ~3.5×106 solar mass black hole, so its orbital motion can be plotted. Nothing is observed at the centre of the observed orbit, the position of the black hole itself—as expected for a black object.

Determining the mass of black holes

Quasi-periodic oscillations can be used to determine the mass of black holes. The technique uses a relationship between black holes and the inner part of their surrounding disks, where gas spirals inward before reaching the event horizon. As the gas collapses inwards, it radiates X-rays with an intensity that varies in a pattern that repeats itself over a nearly regular interval. This signal is the Quasi-Periodic Oscillation, or QPO. A QPO’s frequency depends on the black hole’s mass; the event horizon lies close in for small black holes, so the QPO has a higher frequency. For black holes with a larger mass, the event horizon is farther out, so the QPO frequency is lower.

Black hole candidates

Supermassive black holes at the centres of galaxies.

The jet originating from the centre of M87 in this image comes from an active galactic nucleus that may contain a supermassive black hole. Credit: Hubble Space Telescope/NASA/ESA. According to the American Astronomical Society, every large galaxy has a supermassive black hole at its centre. The black hole’s mass is proportional to the mass of the host galaxy, suggesting that the two are linked very closely. The Hubble Space Telescope and ground-based telescopes in Hawaii were used in a large survey of galaxies.

For decades, astronomers have used the term “active galaxy” to describe galaxies with unusual characteristics, such as unusual spectral line emission and very strong radio emission. However, theoretical and observational studies have shown that the active galactic nuclei (AGN) in these galaxies may contain supermassive black holes.  The models of these AGN consist of a central black hole that may be millions or billions of times more massive than the Sun; a disk of gas and dust called an accretion disk; and two jets that are perpendicular to the accretion disk.

Although supermassive black holes are expected to be found in most AGN, only some galaxies’ nuclei have been more carefully studied in attempts to both identify and measure the actual masses of the central supermassive black hole candidates. Some of the most notable galaxies with supermassive black hole candidates include the Andromeda Galaxy, M32, M87, NGC 3115, NGC 3377, NGC 4258, and the Sombrero Galaxy.

Astronomers are confident that our own Milky Way galaxy has a supermassive black hole at its centre, in a region called Sagittarius A*:
• A star called S2 (star) follows an elliptical orbit with a period of 15.2 years and a pericenter (closest) distance of 17 light hours from the central object.
• The first estimates indicated that the central object contains 2.6M (2.6 million) solar masses and has a radius of less than 17 light hours. Only a black hole can contain such a vast mass in such a small volume.
• Further observations  strengthened the case for a black hole, by showing that the central object’s mass is about 3.7M solar masses and its radius no more than 6.25 light-hours.

Intermediate-mass black holes in globular clusters

In 2002, the Hubble Space Telescope produced observations indicating that globular clusters named M15 and G1 may contain intermediate-mass black holes.  This interpretation is based on the sizes and periods of the orbits of the stars in the globular clusters. But the Hubble evidence is not conclusive, since a group of neutron stars could cause similar observations. Until recent discoveries, many astronomers thought that the complex gravitational interactions in globular clusters would eject newly-formed black holes.

In November 2004 a team of astronomers reported the discovery of the first well confirmed intermediate-mass black hole in our Galaxy, orbiting three light-years from Sagittarius A*. This black hole of 1,300 solar masses is within a cluster of seven stars, possibly the remnant of a massive star cluster that has been stripped down by the Galactic Centre. This observation may add support to the idea that supermassive black holes grow by absorbing nearby smaller black holes and stars.

In January 2007, researchers at the University of Southampton in the United Kingdom reported finding a black hole, possibly of about 10 solar masses, in a globular cluster associated with a galaxy named NGC 4472, some 55 million light-years away.

Stellar-mass black holes in the Milky Way

Artist’s impression of a binary system consisting of a black hole and a main sequence star. The black hole is drawing matter from the main sequence star via an accretion disk around it, and some of this matter forms a gas jet.

Our Milky Way galaxy contains several probable stellar-mass black holes which are closer to us than the supermassive black hole in the Sagittarius A* region. These candidates are all members of X-ray binary systems in which the denser object draws matter from its partner via an accretion disk. The probable black holes in these pairs range from three to more than a dozen solar masses.  The most distant stellar mass black hole ever observed is a member of a binary system located in the Messier 33 galaxy.

Micro black holes

In theory there is no smallest size for a black hole. Once created, it has the properties of a black hole. Stephen Hawking theorized that primordial black holes could evaporate and become even tinier, i.e. micro black holes. Searches for evaporating primordial black holes are proposed for the GLAST satellite to be launched in 2008.

However, if micro black holes can be created by other means, such as by cosmic ray impacts or in colliders, that does not imply that they must evaporate.

The formation of black hole analogues on Earth in particle accelerators has been reported. These black hole analogues are not the same as gravitational black holes, but they are vital testing grounds for quantum theories of gravity. They act like black holes because of the correspondence between the theory of the strong nuclear force, which has nothing to do with gravity, and the quantum theory of gravity. They are similar because both are described by string theory. So the formation and disintegration of a fireball in quark gluon plasma can be interpreted in black hole language. The fireball at the Relativistic Heavy Ion Collider [RHIC] is a phenomenon which is closely analogous to a black hole, and many of its physical properties can be correctly predicted using this analogy. The fireball, however, is not a gravitational object. It is presently unknown whether the much more energetic Large Hadron Collider [LHC] would be capable of producing the speculative large extra dimension micro black hole, as many theorists have suggested.

Now let’s first have a look at two statements made, the first is made by the American astronomical society: every large galaxy has a massive black hole at its centre and, the mass of a black hole is proportional to the host galaxy, suggesting the two are linked.

The model I will present will show this to be the case, but the galaxy is Not the host! The black hole is! And that each galaxy has a black hole will therefore be the logical consequence.

The next is theorized by Stephen Hawking, this theory states that there is no smallest size for a black hole, they could evaporate and become even tinier. While just like the previous statement this will be shown by the model to be correct apart from it evaporating.

The gravitational field, something that is not explained, that lets the apple fall back to the earth, and light not escape from the black hole has to do with the inner configuration and I will get back to this later.

The electromagnetic forces, just like a magnetic field, electricity has its natural flow, in fact it is the same, but everything has a scaling factor related to the golden ratio/mean, planets are more or less in a fixed orbit around the sun, this is due to its own positive and negative field in relation to that of its host and disc which is a galaxy in its large size, planets in a smaller and in case of an atom protons and neutrons. Electrons are bound to the nucleus by what they call an electromagnetic force, likewise, a group of atoms can remain bound to each other forming a molecule.

_________________________________________________________________________________________________

Now the first and very important misconception, a black hole is always portrayed as a two dimensional flat disc, while we look at a 3 dimensional uni-verse, a black hole is Spherical !!!

Let’s go back to Electrons,  like other particles they have properties of both a particle and a wave. The electron cloud is a region inside the potential well where each electron forms a type of three-dimensional standing wave —a wave form that does not move relative to the nucleus. This behaviour is defined by anatomic orbital, a mathematical function that characterises the probability that an electron will appear to be at a particular location when its position is measured. Only a discrete (or quantized ) set of these orbitals exist around the nucleus, as other possible wave patterns will rapidly decay into a more stable form. Orbitals can have one or more ring or node structures, and they differ from each other in size, shape and orientation.

Wave functions of the first five atomic orbitals. The three 2p orbitals each display a single angularnode that has an orientation and a minimum at the centre.

Now keep this torus shape in mind, and move to look at a spherical black hole,

and look at this photo taken by Hubble telescope before explaining more about black holes and the structure of everything.

When we look at a black hole being spherical then it does not reveal a black hole but just a entrance and exit, in other words a north and south pole, that has a field flowing from one to the other with half way the disc where moons, planets and electrons reside.

Again, a sphere like our sun is an event horizon, and the reason why, unlike what science is telling you, that the inner heat of the sun being very high compared to the outer surface is really the opposite. When they look at sunspots they are actually dark, showing less heat, they are a bit like windows into the inner core. Scale and configuration determined its outer appearance.

Science has already shown that an atom is made up of energy and has no material substance, now here comes another clue, it is created by Spirit. Now, do not make it scare you off thinking here we go, religion again. No, spirit is a name given to a pattern that is shown in the picture above, with a circumference of 576 degrees making the shape of an eight on a two dimensional plane, a torus in spin.

Horizontally there is a disc, seen from above it would look something like this, also seen in the blue coloured picture of the black hole further back.

Or like this in a smaller scale,

or an even smaller one,

Now look again at a black hole,

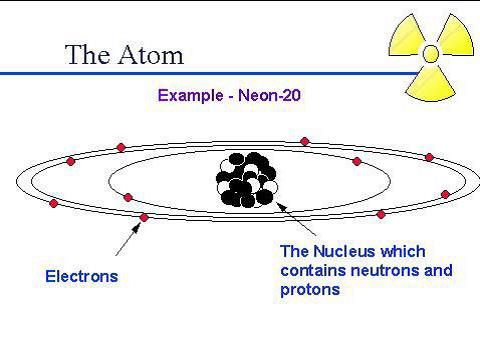
and this, an Atom.

And finally the earth.

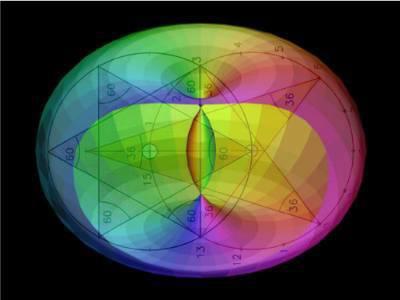
You can clearly see the resemblance between so called black holes, galaxies, solar systems and atoms. So let’s move to the underlying structure in the next image which you can lay over each of them.

Also take into mind that, sunspots, volcanoes the big spot on Jupiter etc. are all located at around 19,2 degrees.
The vertical axis is the centre of the two dimensional picture showing a black hole, but could also be seen as south or north pole.
The star configuration here has reached its perfected state, but they move in relation to each other, you could see it as switching on and off or causing attraction or rejection. In a more fluid state the sphere would show the disc as equator movement (clouds or other atmospherical phenomenon). On the level of DNA this is the switching mechanism or in the case of earth the movement of the pentagram causes friction and movement of plates to cause earthquakes etc.

This pendulum movement is the wave, it is on the level of (freq) consciousness, and is also related to the brain which again has two hemispheres POS/NEG and therefore influences the outcome, acting as a particle or as wave. While this is a simplified presentation which I presented back in 1994, more and more evidence shows that science needs to look at this and include geometry/symmetry but also realise that numbers are more than what meets the eye. The frequency is determined by the geometrical pattern/interrelation between the two, which is the cause of attraction or rejection and matter or light.

All matter is spirit, it is light wave and particle at the same time.
Its geometry is in everything and everything is in it.
144 the elect
414 fountain of life
441 the god of heaven (truth)
18
9
81
1,5×1,5×2,5=5625 18/5,625=32 as in paths
3/0/4/8/0/3=3125 18/3,125=576 (value of spirit and the circumference of the eight)
The 18 and its mirror 81
81/5625=144 x 3125=45
32 paths on each tree making 96 x5625=54/3125=1728 Kali yuga
The Sine of 18 is 0,30901699 x cubit 52,36=16180 golden mean/ratio

This 96 is where the 4 and 5 are located on the eight and at the same time where 36 and 60 degrees come together, 96 is also where the disc or spiral arms of for instance the galaxy originate from.

18×96=1728
1872/52=36 the cubit 52,36
18×72=1296 =12×96=1152 or twice 576 good and evil.

 

10-12-2008

Moshiya van den Broek